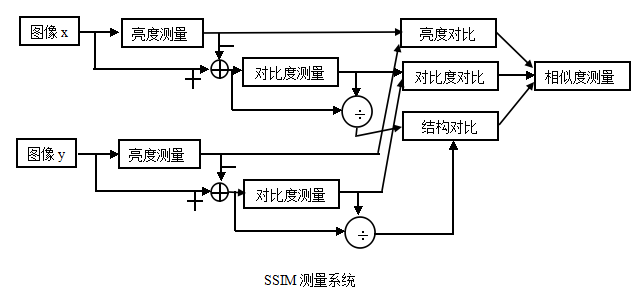
SSIM,IS等生成图像评价指标
IS参考
Inception Score 的基本原理
众所周知,评价一个生成模型,我们需要考验它两方面性能:1. 生成的图片是否清晰 2. 生成的图片是否多样。生成的图片不够清晰,显然说明生成模型表现欠佳;生成的图片够清晰了,我们还要看是不是能生成足够多样的图片,有些生成模型只能生成有限的几种清晰图片,陷入了所谓 mode collapse,也不是好的模型。
Inception Score 是这样考虑这两个方面的:
-
清晰度:把生成的一张图片
输入 Inception V3 中,将输出1000维的向量
,向量的每个维度的值对应图片属于某类的概率。对于一个清晰的图片,它属于某一类的概率应该非常大,而属于其它类的概率应该很小(这个假设本身是有问题的,有可能有些图片很清晰,但是具体属于哪个类却是模棱两可的)。用专业术语说,
的熵应该很小(熵代表混乱度,均匀分布的混乱度最大,熵最大)。
-
多样性:如果一个模型能生成足够多样的图片,那么它生成的图片在各个类别中的分布应该是平均的,假设生成了 10000 张图片,那么最理想的情况是,1000类中每类生成了10张。转换成术语,就是生成图片在所有类别概率的边缘分布
熵很大(均匀分布)。具体计算时,可以先用生成器生成 N 张图片,然后用公式 (1) 的经验分布来代替:
综合上面两方面,Inception Score 的公式为:
:仅仅是为了好看,没有具体含义
:表示从生成器中生成图片
:把生成的图片
输入到 Inception V3,得到一个 1000 维的向量
,也就是该图片属于各个类别的概率分布。IS 提出者的假设是,对于清晰的生成图片,这个向量的某个维度值格外大,而其余的维度值格外小(也就是概率密度图十分尖)。
:N个生成的图片(N 通常取5000),每个生成图片都输入到 Inception V3 中,各自得到一个自己的概率分布向量,把这些向量求一个平均,得到生成器生成的图片全体在所有类别上的边缘分布,见公式 (1)。
:对
和
求 KL 散度。KL 散度离散形式的公式如下:
KL 散度用以衡量两个概率分布的距离,它是非负的,值越大说明这两个概率分布越不像。但这个距离不是对称的,观察公式, 很大
很小的地方对 KL 距离贡献很大,而
很小
很大的地方对 KL 距离的贡献很小。我们预期
的某个维度值很大,而
总体均匀,因此需要把
放在公式 (2) 中双竖线的前面。放到后面可能会造成
的极端值被忽略,而正是这个极端值的存在告诉了我们这个生成的图片是否清晰。
综合起来,只要 和
的距离足够大,就能证明这个生成模型足够好。因为前者是一个很尖锐的分布,后者是一个均匀分布,这俩距离本就应该很大。
公式 (2) 很不直观,在实际操作中可以改成如下形式:
实际操作中,先用生成的大量样本代入公式 (1),求出 ,然后再对每个样本求出
,计算它和
的 KL 散度,最后求平均,再算一下指数即可。(IS越大越好)

IS存在的问题
首先回顾一下 Inception Score 的两个假设:
- 越真实的图片,输入预训练的 Inception V3 ,分类的结果越明确。即在1000维的输出向量中,某一维很大,其余维很小。也就是说,输出的概率分布函数图越尖锐。
- 生成的图片多样性越强,那么类别的边缘分布就越平均,边缘分布的概率函数图像就越平整。
Inception Score 通过计算 1 和 2 中两个概率分布的散度,来衡量生成模型的表现。
我们乍一看这两条假设,不难发现最明显的两个问题:
- 针对第一个假设,是否越真实的图片,分类网络输出的概率分布函数越尖锐?显然是不见得的,如果某一个物体所属的类别在分类网络中并不存在,那么它的分布函数依然尖锐吗?
- 针对第二个假设,是否输出图片均匀地覆盖每个类别,就意味着生成模型不存在 mode collapse?Inception net 输出 1000 类,假设生成模型在每类上都生成了 50 个图片,那么生成的图片的类别边缘分布是严格均匀分布的,按照 Inception Score 的假设,这种模型不存在 mode collapse,但是,如果各类中的50个图片,都是一模一样的,仍然是 mode collapse。Inception Score 无法检测这种情况。
除了上面最直观的两个硬伤,本文开头提到的文章中对 Inception Score 缺点做了详细分析。其中涉及到:使用 IS 时,分类模型应该和生成模型在同一个训练集上训练,否则分类模型计算的边缘分布将不准确,而分类模型对单个图片的预测,也将不能真实反映图片的清晰程度。
出现这一问题的本质原因是:计算 IS 时只考虑了生成样本,没有考虑真实数据,即 IS 无法反映真实数据和样本之间的距离,IS 判断数据真实性的依据,源于 Inception V3 的训练集: ImageNet,在 Inception V3 的“世界观”下,凡是不像 ImageNet 的数据,都是不真实的,都不能保证输出一个 sharp 的 predition distribution。
FID参考
Fréchet Inception Distance (FID)的基本原理
Fréchet Inception Distance (FID) 则是计算了真实图片和假图片在 feature 层面的距离,因此显得更有道理一点。FID 的公式如下:
众所周知,预训练好的神经网络顶层可以提取图片的高级信息,一定程度能反映图片的本质。因此,FID 的提出者通过预训练的 Inception V3 来提取全连接层之前的 2048 维向量,作为图片的特征。公式 (1) 中:
:真实图片的特征的均值
:生成的图片的特征的均值
: 真实图片的特征的协方差矩阵
: 生成图片的特征的协方差矩阵
FID 只把 Inception V3 作为特征提取器,并不依赖它判断图片的具体类别,因此不必担心 Inception V3 的训练数据和生成模型的训练数据不同。同时,由于直接衡量生成数据和真实数据的分布之间的距离,也不必担心每个类别内部只产生一模一样的图片这种形式的 mode collapse。完美避开了很多 Inception Score 的缺陷。
综上所述,对比 IS,FID 有如下优点:
- 生成模型的训练集和 Inception V3 的训练集可以不同。
- 计算 FID 时同时用到了生成的数据和真实数据,比起 IS 来更灵活。可以理解成,IS 判断真实性与否,是把生成数据和 ImageNet 数据做比较,而 FID 是把生成数据和训练数据做比较,因此更 reasonable。
- 以优化 FID 为目标,不会产生对抗样本。因为优化的是 lantent space feature,不是最终的输出图片,不会导致最终的生成图片失真。
FID 仍然存在一些和 IS 同样的问题:
-
FID 只是某一层的特征的分布,是否足以衡量真实数据分布与生成数据分布的距离?同时,提出 FID 公式计算的是多元正态分布的距离,显然神经网络提取的特征并不是多元正态分布。
-
针对同一个生成模型,不同框架下预训练的 Inception V3 算出的 FID 差别是否可以忽略?
-
FID 无法反映生成模型过拟合的情况,如果某个生成模型只是简单拷贝训练数据,FID 会非常小,认为这是一个完美的生成模型,因此,使用 FID 时同时也要通过别的手段证明生成模型没有过拟合。
FID参考
在计算FID中我们也同样使用inception network网络。我们还是先来简单回顾一下什么是inception network,它就是一个特征提取的深度网络,最后一层是一个pooling层,然后可以输出一张图像的类别。在计算FID时,我们去掉这个最后一层pooling层,得到的是一个2048维的高层特征,以下简称n维特征。我们继续简化一下,那么这个n维特征是一个向量。则有:对于我们已经拥有的真实图像,这个向量是服从一个分布的,(我们可以假设它是服从一个高斯分布);对于那些用GAN来生成的n维特征它也是一个分布;我们应该立马能够知道了,GAN的目标就是使得两个分布尽量相同。假如两个分布相同,那么生成图像的真实性和多样性就和训练数据相同了。于是,现在的问题就是,怎么计算两个分布之间的距离呢?我们需要注意到这两个分布是多变量的,也就是前面提到的n维特征。也就是说我们计算的是两个多维变量分布之间的距离,数学上可以用Wasserstein-2 distance或者Frechet distance来进行计算。以下简单介绍一下如何计算这个距离。
假如一个随机变量服从高斯分布,这个分布可以用一个均值和方差来确定。那么两个分布只要均值和方差相同,则两个分布相同。我们就利用这个均值和方差来计算这两个单变量高斯分布之间的距离。但我们这里是多维的分布,我们知道协方差矩阵可以用来衡量两个维度之间的相关性。所以,我们使用均值和协方差矩阵来计算两个分布之间的距离。均值的维度就是前面n维特征的维度,也就是n维;协方差矩阵则是n*n的矩阵。
最后,我们可以使用下面的公式计算FID(看这个公式之前务必要记住这个公式的物理意义,毕竟我们不是专门的数学学习者):
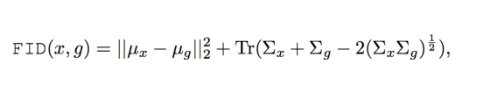 公式中,$T_r$ 表示矩阵对角线上元素的总和,矩阵论中俗称“迹”(trace)。均值为 $\mu$ 协方差为 $\Sigma$ 。此外$x$表示真实的图片,$g$是生成的图片。
公式中,$T_r$ 表示矩阵对角线上元素的总和,矩阵论中俗称“迹”(trace)。均值为 $\mu$ 协方差为 $\Sigma$ 。此外$x$表示真实的图片,$g$是生成的图片。
较低的FID意味着两个分布之间更接近,也就意味着生成图片的质量较高、多样性较好。
FID对模型坍塌更加敏感。相比较IS来说,FID对噪声有更好的鲁棒性。因为假如只有一种图片时,FID这个距离将会相当的高。因此,FID更适合描述GAN网络的多样性。
Structural Similarity(SSIM)的基本原理
SSIM 参考
**SSIM(structural similarity)**结构相似性,也是一种全参考的图像质量评价指标,它分别从亮度、对比度、结构三方面度量两幅图像相似性,其值越大越好,最大为1;作为结构相似性理论的实现,结构相似度指数从图像组成的角度将结构信息定义为独立于亮度、对比度的,反映场景中物体结构的属性,并将失真j建模为亮度、对比度和结构三个不同因素的组合;用均值作为亮度的估计,标准差作为对比度的估计,协方差作为结构相似程度的度量。
与传统检测图像质量的方法MSE,PSNR与人眼的实际视觉感知是不一致的,SSIM算法在设计上考虑了人眼的视觉特性,比传统方式更符合人眼视觉感知,MSE或者是PSNR算法,都是对绝对误差的评估,SSIM是一种基于感知的计算模型,它能够考虑到图像的结构信息在人的感知上的模糊变化,该模型还引入了一些与感知上的变化有关的感知现象,包含亮度mask和对比mask,结构信息指的是像素之间有着内部的依赖性,尤其是空间上靠近的像素点。这些依赖性携带着目标对象视觉感知上的重要信息。
SSIM算法的计算公式:

其中$\mu_x,\mu_y$分别表示图像X和Y的均值,$\sigma_x,\sigma_y$分别表示图像X和Y的方差,$\sigma_{x,y}$表示图像X和Y的协方差,即

最后把三个函数组合起来,得到SSIM指数函数:
这里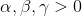
为了得到简化形式,设

即: 
SSIM取值范围[0,1],值越大,表示图像失真越小.
在实际应用中,可以利用滑动窗将图像分块,令分块总数为N,考虑到窗口形状对分块的影响,采用高斯加权计算每一窗口的均值、方差以及协方差,然后计算对应块的结构相似度SSIM,最后将平均值作为两图像的结构相似性度量,即平均结构相似性MSSIM:

由SSIM测量系统可得相似度的测量可由三种对比模块组成,分别为:亮度,对比度,结构。接下来我们将会对这三模块函数进行定义。
首先,对于离散信号,我们以平均灰度来作为亮度测量的估计:
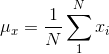
亮度对比函数l(x,y)是关于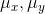
然后,由测量系统知道要把平均灰度值从信号中去除,对于离散信号

对比度对比函数c(x,y)就是
接下来,信号被自己的标准差相除,结构对比函数就被定义成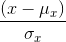
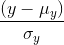
最后,三个对比模块组合成一个完整的相似测量函数:
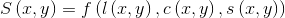
S(x,y)应该满足以下三个条件:
(1) 对称性:
(2) 有界性: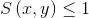
(3) 最大值唯一性:当且仅当x=y时,S(x,y)=1 。
现在,我们定义三个对比函数。
亮度对比函数:
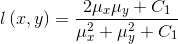
常数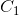
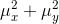
特别的,我们选择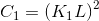
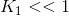
对比度对比函数:
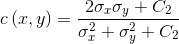
常数
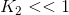
结构对比函数:
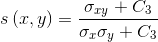
其中

最后把三个函数组合起来,得到SSIM指数函数:
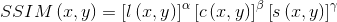
这里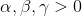
为了得到简化形式,设

LPIPS的基本原理
LPIPS computes the distance between the generated images and reference images at the perceptual domain. It indicates the perceptual difference between the input.