递归的浅显理解

参考

假设我们要计算一个函数：$f(n)=n*f(n-1)$

递归三要素

递归的定义：接受什么参数，返回什么值，代表什么意思 。当函数直接或者间接调⽤⾃⼰时，则发⽣了递归

递归的拆解：每次递归都是为了让问题规模变⼩

**递归的出⼝：**必须有⼀个明确的结束条件。因为递归就是有“递”有“归”，所以必须又有一个明确的点，到了这个点，就不用“递下去”，而是开始“归来”。

1
2

return表示开始返回，即“归”
递归的结束条件十分的重要，在Java中即return回来的的条件

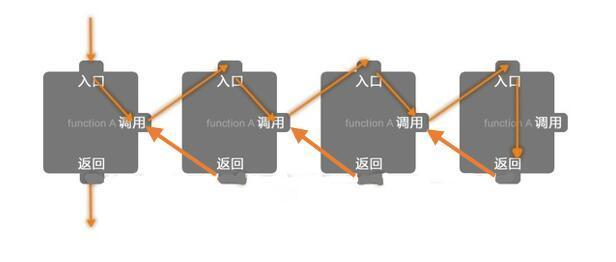
我调用了这个函数，函数需要给我返回一个值，而这个值又取决于我这个函数，只不过函数的变量发生了变化

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/*
     * 请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。
     * https://leetcode-cn.com/problems/dui-cheng-de-er-cha-shu-lcof/
     *
     * 思路：
     * 对于两个对称的结点
     * 如果L.value==R.value &&L.left.value==R.right.value && L.right.value==R.left.value
     *
     * 算法流程：
     * 如果root==null ，直接返回true
     * 否则调用recur(root.left,root.right)
     *
     * recur中的逻辑：
     * 递归终止条件：如果L.value==null && R.value==null 说明自顶向下都对称，返回 true
     *              如果L.value==null || R.value==null || L.value==R.value , 说明不对称，返回false
     *
     * 递归调用：recur(L.left,R.right)&&recur(L.right,R.left)
     * */
    public boolean isSymmetric(TreeNode root) {
        if (root==null) return true;
        else return recur(root.LeftNode,root.RightNode);
    }
    private boolean recur(TreeNode L,TreeNode R){
        if (L==null&&R==null) return true;
        if (L==null||R==null||L.data!=R.data) return false;
        return recur(L.LeftNode,R.RightNode)&&recur(L.RightNode,R.LeftNode);
    }
   

假设给定的二叉树是对称的：

• 从1开始，因为1不为空，所以调用了recur函数，此时recur函数的变量为(2,2),我调用了这个函数，函数需要给我返回一个值，true 或 false

• recur(2,2) 由于都不满足(L==null&&R==null) ；(L==null||R==null || L.data!=R.data)，所以会调用recur(L.LeftNode,R.RightNode)&&recur(L.RightNode,R.LeftNode) ，即recur(3,3)&&recur(4,4)。此时recur(2,2)的值取决于recur(3,3)&&recur(4,4)

  • 其中recur(3,3)由于都不满足(L==null&&R==null) ；(L==null||R==null||L.data!=R.data)，所以会调用recur(L.LeftNode,R.RightNode)&&recur(L.RightNode,R.LeftNode) ，即recur(null,null)&&recur(null,null),此时recur(3,3)的值取决于recur(null,null)&&recur(null,null)

    • 因为recur(null,null)满足了(L==null&&R==null)，所以返回true，所以recur(3,3)==true

  • 其中recur(4,4)由于都不满足(L==null&&R==null) ；(L==null||R==null||L.data!=R.data)，所以会调用recur(L.LeftNode,R.RightNode)&&recur(L.RightNode,R.LeftNode) ，即recur(null,null)&&recur(null,null),此时recur(3,3)的值取决于recur(null,null)&&recur(null,null)

    • 因为recur(null,null)满足了(L==null&&R==null)，所以返回true，所以recur(4,4)==true

• 因为recur(3,3)==true 且 recur(4,4)==true,所以recur(2,2)==true,所以总的返回值为true